扇形周长公式,因为扇形=两条半径+弧长,若半径为r,扇形所对的圆心角为n°,那么扇形周长: c=2r+nπr÷180。 扇形的组成部分: 1、圆上a、b两点之间的的部分叫做"圆弧"简称"弧",读作"圆弧ab"或"弧ab"。 2、以圆心为中心点的角叫做"圆心角"。 弧の長さ=直径×円周率× 中心角 「 中心角 」は、円の中心角360°を全体としたとき、扇形の中心角がどのくらいを占めるかを表す割合です。 公式をつかわない!扇形の中心角の求め方3つのステップ それじゃあ、なぜこの公式で扇形の中心角が求められるのか?? ちょっと気になるよね?? じつは、扇形の中心角の公式は、 比例式をつかった中心角の求め方 から導きだしたものなんだ。
弧长及扇形的面积 圆ppt下载 第一ppt
扇形中心角 求め方 公式
扇形中心角 求め方 公式- 第一个圆黄色区域是一个扇形 一个扇形的面积等于 (角AOB/360°)•π•r² 绿色区 (第二个圆)是一个部分 每块面积相等 扇形的面积减去三角形AOB的面积 查看更多相关 欢迎分享转载→ 弧长公式扇形面积公式积分极坐标高数推导过程 上一篇: 美学公式by空菊无扇形是与 圆形 有关的一种重要 图形 ,其面积与 圆心角 (顶角)、圆半径相关,圆心角为n°,半径为r的扇形面积为nºπr²/360º。 如果其顶角采用弧度单位,则可简化为半径乘弧长乘1/2, 弧长 =半径×弧度)



扇形の中心角の求め方を教えてください 中心角の求め方は2通りのパタ Yahoo 知恵袋
扇形の中心角の求め方 扇形の中心角を求めるには、先ほど説明した面積の公式または弧の長さの公式を利用します。 面積の公式、弧の長さの公式には 中心角の割合 が含まれていましたね。 基本公式: 扇形中心角的弧度数α,扇形半径r,扇形弧长l, α:l=2π:2πr=1:r,(所在圆的周长2πr) l=αr 扇形周长=2rl=2rαr; 中心角を \(x\) とすると、扇形の面積公式を利用し $$\pi \times 6^2\times \frac{x}{360}=12\pi$$ という方程式を作ることができます。 あとは、この方程式を解いていくだけです。 $$\frac{x}{10}=12$$ $$\frac{x}{10}\times 10=12\times 10$$ $$x=1°$$ よって、扇形の中心角は1°となります。
扇形的弧长第二公式为: 扇形的弧长,事实上就是圆的其中一段边长,扇形的角度是360度的几分之一,那么扇形的弧长就是这个圆的周长的几分之一,所以我们可以得出: 扇形的弧长=2πr×角度/360 其中,2πr是圆的周长,角度为该扇形的角度值。扇形中心角怎么算 : 母线²高²=底面圆半径² 以此求出半径,根据周长=2π半径,求出周长,再根据2π母线,求出扇形展开所在圆的周长,两个周长比*360°即为所求角 扇形角度怎么算: 弧长除以周长乘以360等于扇形 已知扇形周长为10cm,面积为6cm^2,求扇形中心角的弧度数同様に、中心角 2° の扇形の面積は、半径が等しい円の面積の360分の2、となるわけですね。 公式の2行目に書いた通り、扇形の面積は、半径 r と弧の長さ l が分かっている場合、次の式で簡単に求められて
そもそも扇形ってどんな形? 中心角を求めよう! 弧の長さの公式を用いた解き方 弧の長さの公式を用いる中心角の求め方 扇形の中心角を求める公式とは? 扇形の面積を求める公式とは? 中心角を出さないと答えが求められない問題ばかりではない 解く 扇形所对圆心角的度数公式 —— 扇形周长公式 因为扇形周长=半径*2一长一短两个弧长若半径为r,直径为d,扇形所对的圆心角的度数为n°,那么扇形周长C=2r(n÷360)πd=2r(n÷180)π r 编辑本段扇形的弧长公式 角度制计算 l=n÷360*2πr=nπr÷180, l是弧长,n是扇形つまり、扇形はあくまで円の一部でしかないということを意識した上で、円についての公式に、一部の修正を加えることからはじめるのです。 もう1度確認します。 扇形の弧は中心角に比例します。 でもさ、それでもやっぱり 比の計算ってちょっと



扇形面积计算公式怎样求扇形面积 有途教育
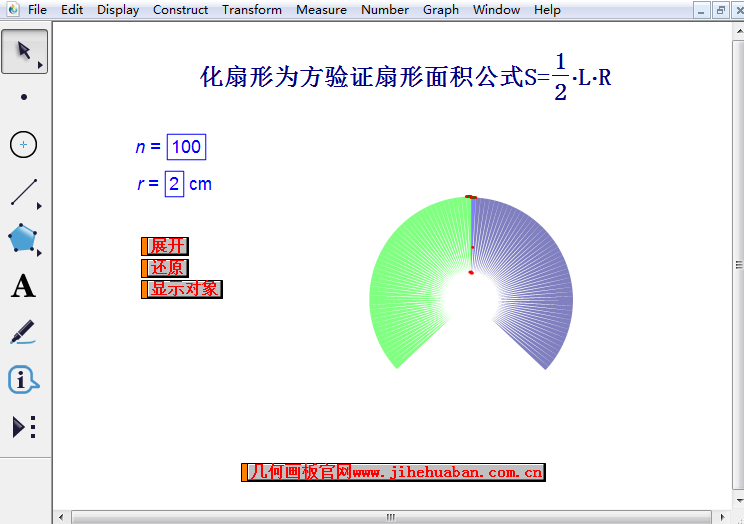



演示扇形面积公式推导过程
兩圓相交面積公式,大家都在找解答。 創易E學中心國二下四扇形重疊圖形 两个圆形交叉的地方的面积如何计算 首页 ·圆心角是指在中心为o的圆中,过弧ab两端的半径构成的∠aob, 称为弧ab所对的圆心角。 圆心角等于同一 弧 所对的 圆周角 的二倍。 1 扇形计算公式(fan area formula)是几何中用来计算扇形面积的公式。 一条弧和经过这条弧两端的两条半径所围成的图形叫扇形(半圆与直径的组合也是扇形)。 显然, 它是由圆周的一部分与它所对应的圆心角围成。 《几何原本》中这样定义扇形:由顶点在圆心的角的两边和这两边所截一段圆弧围成的图形。 扇形计算公式 如何获得 中文名 扇形面积公式 展开




怎么计算圆的半径 最有妙招网




扇形の中心角の求め方を教えてください Clear
扇形周长公式为:扇形周长=扇形半径×2弧长,即C=2r(n÷360)πd=2r(n÷180)πr。 解答过程 因为扇形周长=半径×2弧长,若半径为r,直径为d,扇形所对的圆心角的度数为n°,那么扇形周长:C=2r(n÷360)πd=2r(n÷180)πr。 扇形其他公式 扇形的弧长公式 扇形弧长是圆周长的一部分。 周长=2πr 每度所对应的弧长是:2πr÷360=πr÷180 每弧度所对应的弧长是:2πr÷2π=r 已知度数α,求扇形弧长公式是:απr÷180 已知弧度β,求扇形弧长公式是:βr中心角の公式は、 x = 180L/πr だったよね?おうぎ形の弧の長さ、面積、中心角の求め方と公式 おうぎ形は円を切りとったものです。 半分だけ切りとれば中心角は180°、さらに半分切りとれば中心角は90°になります。 ケーキを半分に切ったり、三分の一にしたりするときを想像するとわかりやすいでしょう。 おうぎ形の弧の長さと面積は下のプリントのように求めます。 半径をr、中心角をa°とします。 弧




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




扇形的面积计算公式扇形的面积公式是什么如何计算扇形的面积
・円弧の長さは rθ 円周の長さ 2πr に対して、中心角の割合が θ/2π であるため もしくは、単純に、1ラジアンの円弧の長さ(=半径(r))の θ倍であるため ・扇形の面積は (r 2 θ)/2円弧三角計算 半径、中心角(DMS形式orDEG形式)、弦長、弧長、高さ、底辺1、底辺2、円弧高を求める計算です。请问扇形的面积公式和周长公式分别是那个跟那个啊? 若半径为R,扇形所对的圆心角为n°,那么扇形周长: C=2R+nπR÷180 编辑本段扇形面积公式 在半径为R的圆中,因为360°的圆心角所对的扇形的面积就是圆面积S=πR^2,所以圆心角为n°的扇形面积: S=nπR^2÷360角度制计算: l= (n÷180)×π×r, l是弧长,n是扇形圆心角,π是圆周率,r是扇形半径 弧度制计算: l=α×r ,l是弧长,α是弧l所对的圆心角的弧度数的绝对值,r是半径 3、扇形面积计算公式 S=(n÷360)×π×r ^2 π是圆周率,r是扇形的半径,n是圆心角的度数 扇形面积=半径×半径×圆周率×圆心角度数÷360 S=nπR^2/360 S=1/2LR R是扇形半径,n是弧所对圆周角度数,π是圆周率



1 设圆的半径为r圆心角为n度 那么扇形面积s扇形是圆面积s的360分之 扇形的面积公式 1 设圆的半径为r圆心角为n度 那么扇形面积s扇形是圆面积s的360分之 扇形的面积公式为 S 作业 慧海网




扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ
扇形の中心角の求め方がわからない! 比例を理解できれば公式 ★扇形の中心角の求め方★途中式をていねいに解説!面積、弧 扇形の中心角の求め方の公式ってなんですか? 知恵袋で 3分で分かる!中心角の求め方ー公式とその証明、練習問題扇形の中心角を求める公式を教えてください! 出来ればSやLなどのアルファベットでは無く半径や、直径などの言葉で教えてくれたら嬉しいです! 面積 扇形 中1 この長さ 公式 q1~q4は、約分した分数を見て、即座に中心角が答えられるようにしておきましょう。 q5のような瞬間的に角度が思いつきにくい分数については、公式に当てはめて8秒以内に解答できれば問題ありません。 次の記事 ⇒ 三角錐の体積比を楽に求められる公式




扇形的面积 弧长 周长 弦长在线计算器 三贝计算网 23bei Com



Led屏各种面积计算办法汇总点击查看 临沂led Led显示屏 临沂全彩显示屏 枣庄led 泰安led 日照led大屏幕 航空箱 航空箱厂家 航空箱生产厂家 山东鹰视电子科技有限公司
扇形 扇形の面積を求める公式は、次の通りです。 S = πr2 × x 360 = 1 2lr S = π r 2 × x 360 = 1 2 l r 中心角 x°、半径 r の扇形 ここで、S は扇形の面積、π は円周率、r は円の半径、x は中心角(単位「度」)を表します。 また、2行目の l は扇形の弧の長さを表し编辑分类 扇形计算公式是一条弧和经过这条弧两端的两条半径所围成的图形叫扇形(半圆与直径的组合也是扇形)。 显然, 它是由圆周的一部分与它所对应的圆心角围成。 《几何原本》 中这样定义扇形:由顶点在圆心的角的两边和这两边所截一段圆弧围成α: 扇形面积=2π:πr²=2r²,(所在圆的面积πr²) 扇形面积=αr²/2 希望能解决您的问题。




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



扇形中心角公式 西瓜视频搜索
在问 C、D为两圆交点。 两个扇形面积减去两个三角形面积等于阴专影部分属面积,即为两圆交叉重合部分面积。 已赞过 扇形弧长公式是什么?这要取决于已知条件。 扇形弧长是圆周长的一部分。 周长=2πr 每度所对应的弧长是:2πr÷360=πr÷180 每弧度所对应的弧长是:2πr÷2π=r 已知度数α,求扇形弧长公式是:απr÷180 已知弧度β,求扇形弧长公式是:βr扇形圆心角的弧度数公式 : 圆心角的弧度=圆心角对应的弧长÷半径 弧长是正数,所以圆心角的弧度不能是负数,而且就是那个扇形对应的角度,不能再加减2π因为如果再加2π,那对应的扇形应该是超过了一个圈再的扇形




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 リョースケ大学



扇形的体积公式 土嘎嘎
扇形弧长公式是什么?这要取决于已知条件。 扇形弧长是圆周长的一部分。 周长=2πr 每度所对应的弧长是:2πr÷360=πr÷180 每弧度所对应的弧长是:2πr÷2π=r 已知度数α,求扇形弧长公式是:απr÷180 已知弧度β,求扇形弧长公式是:βr 扇形面积公式 在半径为R的圆中,因为360°的圆心角所对的扇形的面积就是圆面积S=πR^2,所以圆心角为n°的扇形面积: S=nπR^2÷360 扇形还有另一个面积公式 S=1/2lR 其中l为弧长,R为半径 扇形的弧长公式 l= (n/180)*pi*r,l是弧长,n是扇形圆心角,pi是圆周率,r 扇形面积公式:S=IR/2 S扇=(lR)/2 (l为扇形弧长) =(1/2)θR²(θ为以弧度表示的圆心角) S扇=(n/360)πR² s扇=1/2lr(当知道弧长时) (n为圆心角的度数,R为扇形的半径) 注:π为圆周率约等于 一般取314 扩展资料: 一、公式推导过程 因为圆形为360度,扇形




おうぎ形の弧長 面積 中心角 半径 具体例で学ぶ数学



圆锥侧面积公式推导图圆锥侧面积计算公式 朵拉利品网



扇形面积计算公式讲解 北京爱智康




扇形中心角公式 ニスヌーピー壁紙




1 1 2 4 扇形面积公式 高中数学必修4 高中数学 辅立码课



圆弧面积计算公式图解 图片欣赏中心 急不急图文 Jpjww Com



弧长及扇形的面积 圆ppt下载 第一ppt



扇形的周长公式 扇形的周长公式 三人行教育网 Www 3rxing Org



扇形面积计算圆扇形弧形计算公式谁有计算圆弧长扇形面积和圆锥的面积的公式 尚书坊




如何求弧长 10 步骤 包含图片



扇形面积公式三种 搜狗图片搜索



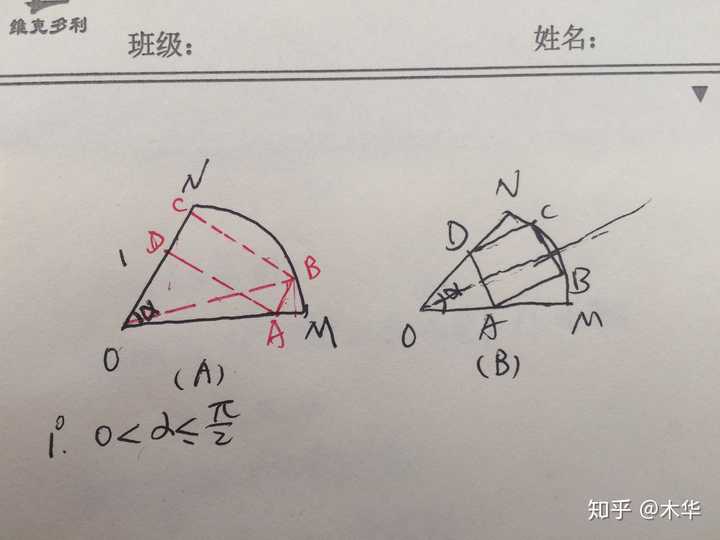
类比教学到底教什么




扇形面积的计算公式 扇形的面积计算公式



弧长和扇形面积计算公式扇形弧长的计算公式 爱华网



3 9 弧长及扇形的面积 哔哩哔哩 つロ干杯 Bilibili



圆形面积圆的面积公式是什么 大业商务网



扇形面积公式 弧长公式与扇形面积公式 尚书坊




扇形面積公式三角函數數學科 Rlnew



扇形面积公式推导图片 搜狗图片搜索




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



扇形弧长公式计算方法 北京爱智康
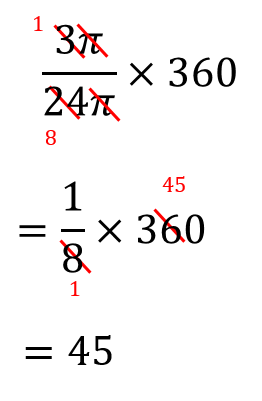



おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ




数 你好看 任意角三角函数与诱导公式 知乎




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



圆锥公式大全圆锥的全部公式 朵拉利品网




Ppt 弧长和扇形面积powerpoint Presentation Free Download Id



已知扇形的面积为2 扇形圆心角的弧度数是4 则扇形的周长为 高中一年级 数学试题 弧度制 弧度与角度的互化考点 好技网



扇形面积的计算公式的应用 28 5弧长和扇形面积的计算 初中冀教版13版 数学中国网 Mathschina Com




おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典



扇形面积计算公式 万图壁纸网




扇形面积计算公式如何推导 教育频道 手机搜狐




Ppt 24 4 1 弧长和扇形面积powerpoint Presentation Free Download Id



扇形中心角公式 西瓜视频搜索



扇形中心角公式 西瓜视频搜索



弧长公式 腾讯视频
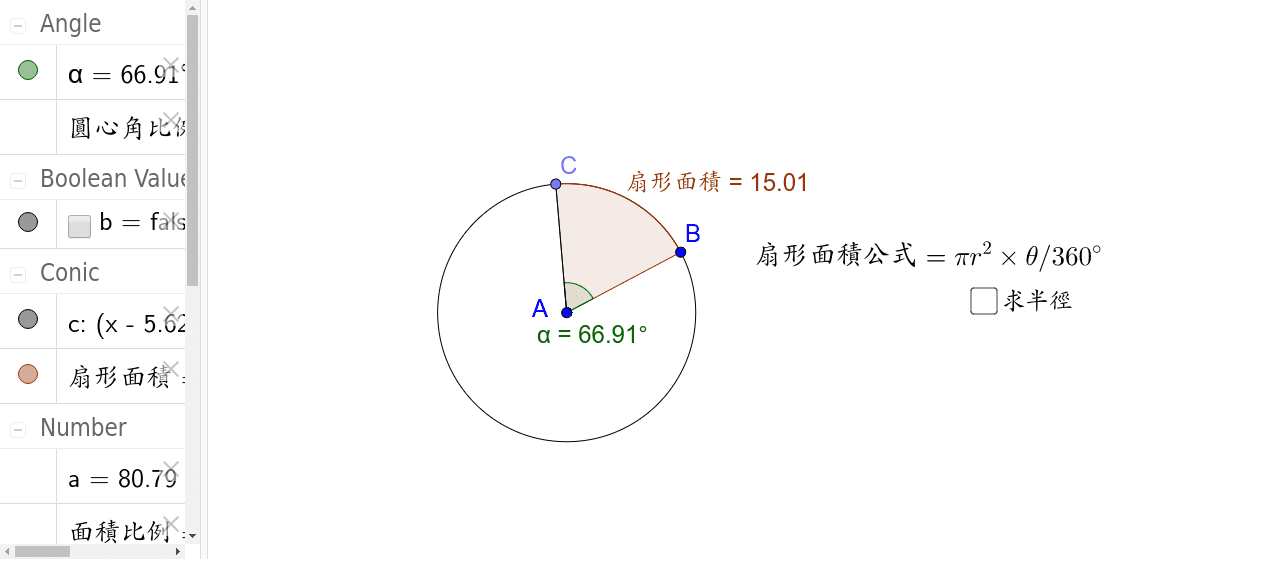



扇形面積公式2 Geogebra



扇形弧长公式 扇形弧长公式画法




面積 40 由圓心角來求扇形大小 Youtube




数学必修四知识点总结ppt课件下载 Ppt模板 爱问共享资料




扇形计算公式 搜狗百科




B Lr8f8asdwonm




19 年高三数学第26课时任意角的三角函数教案下载 Word模板 爱问共享资料



Search Q E5 A6 E9 95 Bf E5 85 Ac E5 8f Tbm Isch




第三单元三角函数 解三角形 Ppt Download




円 扇形 の面積 周や弧の長さの公式 数学fun



扇形计算公式讲解 北京爱智康




Tjs9ivb6o057jm



扇形的认识计算 腾讯视频
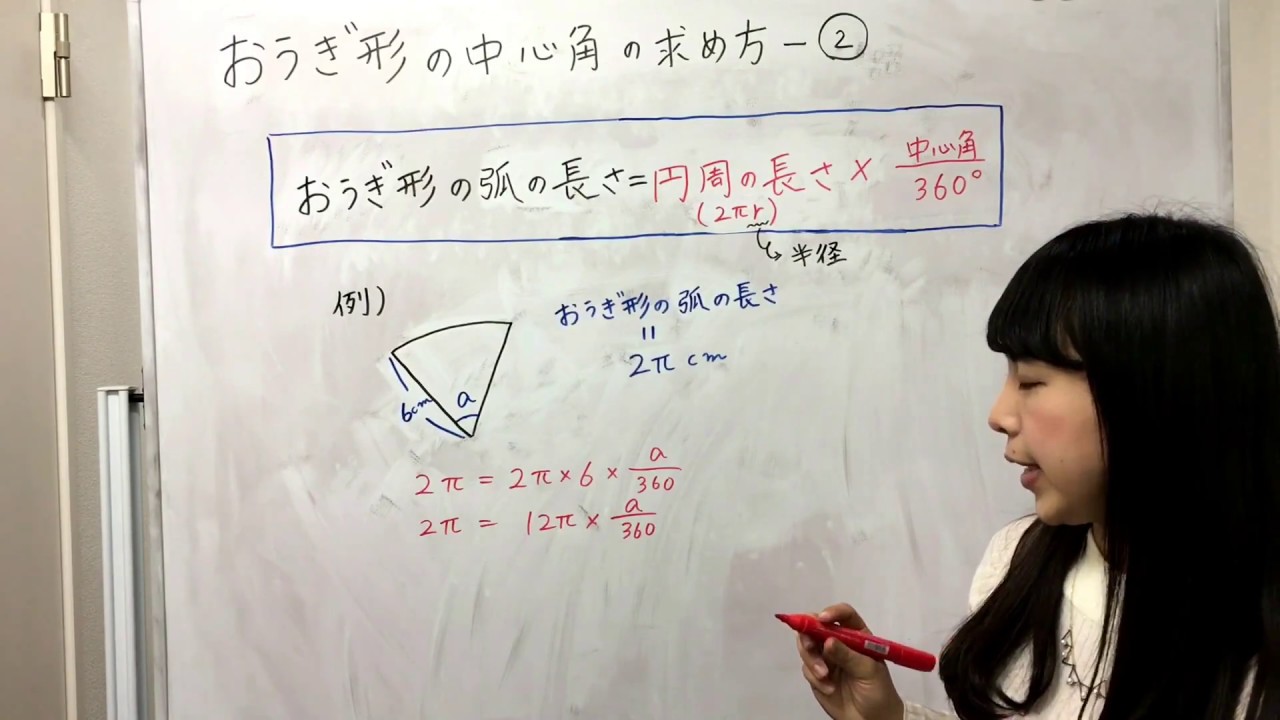



中1数学 おうぎ形の中心角の求め方 家庭教師のガンバ Youtube




基礎 給扇形面積求圓心角 Youtube



扇形中心角 高中数学综合论坛 中学生答疑交流论坛 上海腾飞教育学习论坛




扇形的面积怎么求 百度经验




一课一练 5 5六年级上册数学 扇形 半径 圆心角 弧长 网易订阅



1




扇形漏斗的体积怎么算 漏斗的扇形怎样计算 三人行教育网 Www 3rxing Org



1




圆中有关计算 弧长 扇形面积和圆锥




三角函数小题 基本公式及变换专题 知乎



百分比扇形圆心角公式 初中扇形圆心角公式 扇形圆心角度数怎么求




扇形面積公式弧長14 Zilhc



扇形中心角公式 西瓜视频搜索



高考数学三角函数大总结 例题 解析




類題15求解 扇形半徑為30 中心角60度 則內切圓半徑為何 Clear



扇形的面积公式 哔哩哔哩 つロ干杯 Bilibili




中心角の求め方が即わかる 合わせて知りたい知識とは 高校生向け受験応援メディア 受験のミカタ



扇形弦长计算公式图扇形弦长计算公式 尚书坊



圆心角弧度数公式 扇形中心角的弧度数公式 贝奈网



九年级数学上册24 3圆与多边形4弧长扇形面积圆锥表面积计算课件 新人教版 莲山课件




弧度制 教案5下载 Word模板 爱问共享资料



扇形中心角公式 西瓜视频搜索



半径9cm 面積18pcm の扇形の中心角を求めなさいという問 Yahoo 知恵袋




圆锥的表面积与体积




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット



扇形面积公式 腾讯视频




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




圆心角的弧度数公式 搜狗搜索



三角函数弧长和扇形面积公式 哔哩哔哩 Bilibili




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ



Q Tbn And9gcr 1plm97jyydvtyw4s3scmkwn6dg6hh Hm Jjs9o4zwiusl2nz Usqp Cau



扇形の中心角の求め方を教えてください 中心角の求め方は2通りのパタ Yahoo 知恵袋




已知一扇形中心角为x 所在圆的半径为r 1 若x Pai 3 R 2cm 求扇形的弧长及该弧所在弓形的面积 2 若扇形周



扇形面積計算公式第二章三角函數 rbmi



扇形面积计算计算方法 北京爱智康




扇形弧长公式扇形弧长公式扇形弧长介绍




扇形の中心角の求め方 途中式をていねいに解説 面積 弧の長さから求める方法 中学数学 理科の学習まとめサイト




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ


